Información sobre el curso

El propósito de este curso es repasar los fundamentos esenciales del cálculo diferencial, que son indispensables para los primeros años de cualquier carrera universitaria que involucre matemáticas. Nuestra meta es ofrecer un curso elemental acerca de las funciones y las derivadas, abarcando también sus aplicaciones.

¿Qué aprenderás en este curso?

En el ámbito de las matemáticas, el concepto de función es fundamental. Una función es una relación entre dos conjuntos, en la cual a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Las funciones pueden ser representadas mediante una fórmula matemática, una tabla de valores o un gráfico. Las operaciones con funciones son procesos que nos permiten realizar diversas manipulaciones y análisis de las mismas. Estas operaciones incluyen la suma, resta, multiplicación y división de funciones, así como la composición de funciones. Estas operaciones nos ayudan a simplificar expresiones, encontrar dominios y rangos, y resolver ecuaciones funcionales. Por otro lado, la derivada es un concepto fundamental en el cálculo diferencial. La derivada de una función nos indica cómo cambia el valor de la función en relación a cambios infinitesimales en su variable independiente. La derivada se representa mediante el símbolo “d/dx” y se calcula mediante límites y reglas específicas. La derivada tiene diversas propiedades que nos permiten simplificar su cálculo y realizar análisis más profundos de las funciones. Estas propiedades incluyen la regla de la suma, la regla del producto, la regla del cociente y la regla de la cadena. Estas propiedades nos ayudan a encontrar puntos críticos, determinar la concavidad de una función y trazar la gráfica de una función. 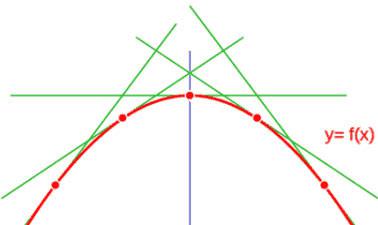Una aplicación importante del cálculo d iferencial es el cálculo de máximos y mínimos de funciones. Estos puntos extremos nos indican los valores máximos y mínimos que puede alcanzar una función en un determinado intervalo. Para encontrar estos puntos, utilizamos la derivada de la función y la igualamos a cero. Luego, analizamos los puntos críticos y los puntos de inflexión para determinar si son máximos o mínimos. Además de los máximos y mínimos absolutos, también existen los máximos y mínimos condicionados. Estos puntos extremos están sujetos a una restricción o condición adicional. Para encontrar estos puntos, utilizamos el método de los multiplicadores de Lagrange, que nos permite encontrar los valores extremos de una función sujeta a una o varias restricciones. En resumen, el concepto de función y las operaciones con funciones son fundamentales en matemáticas. La derivada y sus propiedades nos permiten analizar el cambio de una función, mientras que el cálculo de máximos y mínimos nos ayuda a encontrar los valores extremos de una función. Los máximos y mínimos condicionados, por su parte, nos permiten encontrar los valores extremos sujetos a restricciones adicionales. Estos conceptos y técnicas son ampliamente utilizados en diversas áreas de la ciencia y la ingeniería.